Байесовский вывод - интуиция и примеры
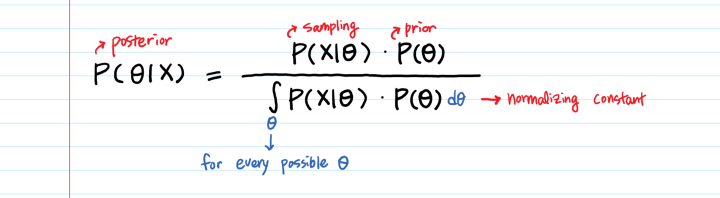
Часть 1, Часть 2, Часть 3
Зачем кто-то вообще изобрел байесовский вывод?
Чтобы обновлять вероятность по мере поступления новых данных.
Суть байесовского вывода в том, чтобы объединить два разных распределения (вероятности и априорное) в более “умное” (апостериорное). Апостериорное умнее в том смысле, что классический метод максимального правдоподобия не принимает в расчет априорное распределение. Мы используем апостериорную вероятность для поиска “наилучших” параметров; “наилучших” в терминах оценки апостериорного максимума с учетом данных. Этот процесс называется оценка апостериорного максимума. Оптимизация, используемая в оценке апостериорного максимума, та же, что и в типичном машинном обучении (градиентный спуск, метод Ньютона и так далее).
Довольно легко понять знаменитое уравнение Байеса аналитически. Но как использовать его с данными?
Одно из самых знаменитых уравнений в мире статистикиУ нас будет большое количество точечных данных X. Как перемножить вероятность относительно X и вероятность относительно θ? Получится слишком много возможных комбинаций θ и X.
Искусство байесовского вывода состоит в том, как вы его реализуете.
Пример
Мой блог посещает примерно 2,000 человек в день. Кто-то ставит лайк после прочтения, кто-то — нет. Я бы хотела спрогнозировать количество людей, которые поставят лайк, когда я опубликую новую статью. Данные о лайках, которые я собираю — двоичные: 1 означает лайк, 0 — отсутствие лайка.
Задачи такого типа широко применимы. Попробуйте использовать их в собственной работе по моделированию — для расчета рейтинга кликов вашей рекламы, коэффициента конверсии клиентов, фактически купивших что-то на вашем сайте, процента людей, согласившихся пойти с вами на свидание, шансов на выживание женщин с раком груди и так далее.
Генерация данных:
Давайте сгенерируем данные X.(В реальной жизни вы никак не контролируете X, только наблюдаете.)
import numpy as np
np.set_printoptions(threshold=100)
# Генерируем 2,000 читательских ответов.
# Предполагаем, что количество лайков следует процессу Бернулли - последовательности двоичных (успех или неудача) случайных переменных.
# 1 означает лайк, 0 - отсутствие лайка
# Устанавливаем уровень успеха в 30%.
clap_prob = 0.3
# IID (независимое и равномерно распределенное) условие
clap_data = np.random.binomial(n=1, p=clap_prob, size=2000)
In [1]: clap_data
Out[1]: array([0, 0, 0, ..., 0, 1, 0])
In [2]: len(clap_data)
Out[2]: 2000
Байесовский вывод состоит из трех шагов.
Шаг 1. [Априорная вероятность] Выбираем плотность вероятности, чтобы смоделировать параметр θ, то есть априорное распределение P(θ). Это наше лучшее предположение о параметрах до того, как мы получим данные X.
Шаг 2. [Функция вероятности] Выбираем плотность вероятности для P(X|θ). По сути мы моделируем, как данные X будут выглядеть с заданным параметром θ.
Шаг 3. [Апостериорная вероятность] Вычисляем апостериорное распределение P(θ|X) и выбираем θ с самой высокой P(θ|X).
В итоге апостериорное распределение становится новым априорным распределением. Третий шаг нужно повторять каждый раз при поступлении новых данных.
Шаг 1. Априорная вероятность P(θ)
Первый шаг — это выбор плотности вероятности для моделирования параметра θ.
Что отображает параметр θ?
Вероятность лайков ???? .
Какие распределения вероятностей стоит использовать для моделирования вероятности?
Чтобы отобразить вероятность, нужно выполнить несколько условий. Во-первых, область определения должна быть между 0 и 1. Во-вторых, распределение должно быть непрерывным.
Хорошо подойдут два распределения: бета-распределение и распределение Дирихле.
Дирихле — многомерно, бета — одномерно. Нам нужно предсказать только одну вещь — вероятность. Давайте используем бета-распределение (Бета-распределение: интуиция, примеры, вывод).
(Интересное замечание: очень легко создать произвольное распределение по (0, 1). Просто возьмите любую функцию, с областью значений между 0 и 1, а затем проинтегрируйте ее от 0 до 1 и разделите функцию на результат.)
Чтобы использовать бета-распределение, нужно определить два параметра — α и β. В нашем случае α — количество людей, поставивших лайк (число успешных исходов), а β — количество людей, не поставивших лайк (число неудач). Эти параметры — насколько они велики или малы— определяют форму распределения.
Скажем, у вас есть данные за вчерашний день: из 2,000 посетителей лайк поставили 400. Как записать это в терминах бета-распределения?
import scipy.stats as stats
import matplotlib.pyplot as plt
a = 400
b = 2000 - a
# область определения θ
theta_range = np.linspace(0, 1, 1000)
# априорное распределение P(θ)
prior = stats.beta.pdf(x = theta_range, a=a, b=b)
Давайте начертим априорное распределение по всем значениям θ.
# Строим априорное распределение
plt.rcParams['figure.figsize'] = [20, 7]
fig, ax = plt.subplots()
plt.plot(theta_range, prior, linewidth=3, color='palegreen')
# Добавляем заголовок
plt.title('[Prior] PDF of "Probability of Claps"', fontsize=20)
# Добавляем метки X и y
plt.xlabel('θ', fontsize=16)
plt.ylabel('Density', fontsize=16)
# Добавляем разметку
plt.grid(alpha=.4, linestyle='--')
# Рисуем чертеж
plt.show()
Не знакомы с термином “Density” (плотность) оси Y? → Читайте статью “Плотность вероятности не есть сама вероятность”.
Как и ожидалось, функция резко возрастает на 20% (400 лайков / 2,000 читателей). 2,000 точечных данных, как видим, дают весьма сильную априорную вероятность. Если мы используем меньшее количество данных, скажем, 100 читателей, пик будет выглядеть значительно менее резким. Попробуйте с α = 20 и β = 80.
Для тех, кого интересует ответ на вопрос, как плотность вероятности может быть больше 1 ????“Плотность вероятности не есть сама вероятность”.
Шаг 2. Функция вероятности P(X|θ)
Выбираем модель вероятности для P(X|θ) — вероятность просмотра данных X задается параметром θ. Функция вероятности также называется выборочным распределением. Для меня термин “выборочное распределение” значительно более интуитивно понятен, чем “функция вероятности”.
Чтобы выбрать, какое распределение использовать для моделирования выборочного распределения, нужно задаться вопросом:
Как выглядят наши данные X?
X — это двоичный массив [0,1,0,1,...,0,0,0,1].
У нас также есть общее количество посетителей (n) и количество лайков, следовательно, вероятность лайков (p) от X.
Хорошо, n и p…Очевидно это..?
Биномиальное распределение с n и p для прогнозирования количества лайков.
# Выборочное распределение P(X|θ) с заданной clap_prob(θ)
likelihood = stats.binom.pmf(k = np.sum(clap_data), n = len(clap_data), p = clap_prob)
Давайте посмотрим на график P(X|θ) для всех возможных X и заданной θ(=0.3).
# Область определения (количество лайков)
X = np.arange(0, len(clap_data)+1)
# Правдоподобие P(X|θ) для всех X
likelihood = stats.binom.pmf(k = X, n = len(clap_data), p = clap_prob)
# Чертим график
fig, ax = plt.subplots()
plt.plot(X, likelihood, linewidth=3, color='yellowgreen')
# Добавляем заголовок
plt.title('[Likelihood] Probability of Claps' , fontsize=20)
# Добавляем метки X и y
plt.xlabel(’X’, fontsize=16)
plt.ylabel(’Probability’, fontsize=16)
# Добавляем разметку
plt.grid(alpha=.4, linestyle='--')
# Отображаем чертеж
plt.show()
Функция правдоподобия P(X|θ) с единственным заданным θ = 30%
Это вероятность увидеть X успешных исходов в n попыток при условии, что θ = 30%.
Шаг 3. Апостериорная вероятность. P(θ|X)
Наконец, давайте ответим на вопрос, заданный в начале статьи: зачем нам байесовский вывод?
У нас будет большое количество точечных данныхX. Как перемножить вероятностьотносительно X и вероятность относительно θ? Получится слишком много возможных комбинаций θ и X.
Весь смысл байесовского вывода заключается в том, чтобы найти наиболее соответствующую данным θ.
Наше начальное предположение о параметрах было P(θ). По мере поступления новых данных мы превращаем простую P(θ) в нечто более информативное — P(θ|X). P(θ|X) — все еще вероятность θ, такая же как P(θ). Однако P(θ|X) “умнее” P(θ).
Как перемножить вероятностьотносительно X и вероятность относительно θ?
Вычисляем P(θ) и P(X|θ) для заданного значения θ и перемножаем их. Если сделать это для каждой возможной θ, мы сможем выбрать наибольшее P(θ) * P(X|θ) среди различных θ.
Мы можем умножить P(θ) на P(X|θ) по условию θ.
Код стоит тысячи слов:
# (cont.)
theta_range_e = theta_range + 0.001
prior = stats.beta.cdf(x = theta_range_e, a=a, b=b) - stats.beta.cdf(x = theta_range, a=a, b=b)
# prior = stats.beta.pdf(x = theta_range, a=a, b=b)
likelihood = stats.binom.pmf(k = np.sum(clap_data), n = len(clap_data), p = theta_range)
posterior = likelihood * prior
normalized_posterior = posterior / np.sum(posterior)
fig, axes = plt.subplots(3, 1, sharex=True, figsize=(20,7))
plt.xlabel('θ', fontsize=24)
axes[0].plot(theta_range, prior, label="Prior", linewidth=3, color='palegreen')
axes[0].set_title("Prior", fontsize=16)
axes[1].plot(theta_range, likelihood, label="Likelihood", linewidth=3, color='yellowgreen')
axes[1].set_title("Sampling (Likelihood)", fontsize=16)
axes[2].plot(theta_range, posterior, label='Posterior', linewidth=3, color='olivedrab')
axes[2].set_title("Posterior", fontsize=16)
plt.show()
Посмотрите внимательно на третий график апостериорной вероятности: вероятность сместилась к априорной. Вероятность лайка для априорного распределения была 20%. Вероятность для заданных данных — 30%. Пик апостериорной вероятности где-то около 0.25%.
Также заметьте, что ширина колокола кривой в априорной вероятности и функции вероятности уменьшилась в апостериорной вероятности. Диапазон возможных параметров стал уже, поскольку мы включили больше информации в процессе выборки.
Чем больше у нас данных, тем сильнее график апостериорной вероятности будет похож на график функции вероятности, а не на график априорной вероятности. Другими словами, чем больше у вас данных, тем меньше значит изначальное априорное распределение.
Наконец, мы выбираем θ, дающую наибольшую апостериорную вероятность, вычисленнуючисленной оптимизацией (такой как градиентный спуск или метод Ньютона). Полностью вычислительный процесс называется оценка апостериорного максимума.
Примечание: мы вычислили априорную вероятность, вычитая два stats.beta.cdf вместо использования stats.beta.pdf, потому что вероятность stats.binom.pmf— это именно вероятность, а stats.beta.pdf возвращает плотность вероятности. Даже если мы используем плотность вероятности для вычисления апостериорной вероятности, результат оптимизации не изменится. Однако, чтобы они соответствовали друг другу, необходимо преобразовать плотность в вероятность.
Несколько замечаний:
Нет. Максимум можно найти и без нормализации. Однако, если вам нужно сравнить апостериорные вероятности из разных моделей или рассчитать точечные оценки, нормализация необходима.
4. Оценка апостериорного максимума может рассматриваться как регуляризованное максимальное правдоподобие с включением дополнительной информации.
5. Вы уже знакомы с оценкой максимального правдоподобия, но не достаточно с оценкой апостериорного максимума? Оценка максимального правдоподобия — просто частный случай оценки апостериорного максимума с равномерным распределением.
6. Я написала “Априорное распределение — это наше лучшее предположение о параметрах до того, как мы получим данные”, однако на практике, как только мы вычисляем апостериорную вероятность, она становится новой априорной до поступления следующей порции данных. Таким образом мы последовательно обновляем априорную и апостериорную вероятности. На этой идее базируются методы Монте-Карло на основе цепей Маркова.
Перевод статьи Aerin Kim: Bayesian Inference — Intuition and Example
Комментарии