QR-разложение матрицы
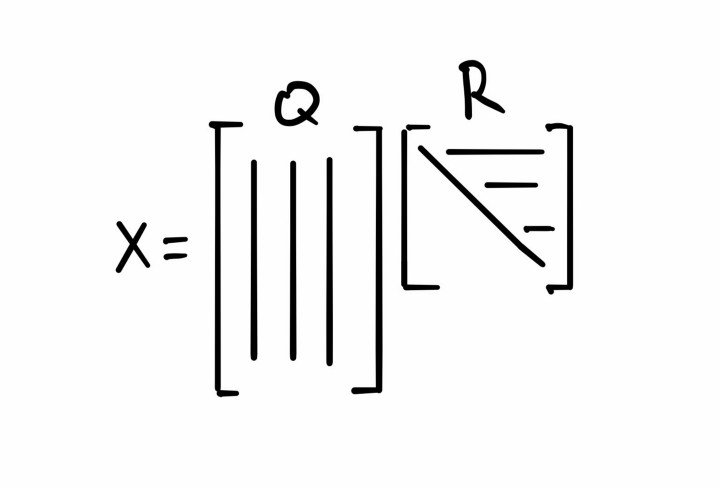
Наука о данных и разложение матриц
Специалистам по данным стоит хорошо знать несколько разложений матриц, потому что они помогают находить методы для актуальных вычислений и оценки результатов для моделей и алгоритмов, с которыми мы работаем. В некоторых случаях конкретной формой разложения является алгоритм (например, в методе главных компонент и сингулярном разложении). И во всех случаях разложение матриц помогает развивать интуицию и способность к анализу.
QR—разложение — одно из самых полезных. Ему находится множество важных применений в науке о данных, статистике и анализе данных. Одно из подобных применений — вычисление решения задачи наименьших квадратов.
Содержание статьи
- Повторение проблемы наименьших квадратов.
- Описание с QR-разложения.
- Решение задачи наименьших квадратов с помощью QR-разложения.
- Реализация вычисления QR-разложения на R и C++ и сравнение реализаций.
Задача наименьших квадратов
QR-разложение позволяет вычислить решение задачи наименьших квадратов. Подчеркиваю, именно вычислить, поскольку обычный метод наименьших квадратов дает нам закрытое решение в форме нормальных уравнений. Это замечательно, но, если нам нужно найти актуальное числовое решение, этот метод не подойдет.
Вспомним задачу наименьших квадратов. Нужно решить уравнение ниже:
Проблема состоит в том, что не существует решения для β, потому что обычно, если у нас больше наблюдений, чем переменных, X не имеет обратного значения, следовательно, вычисление ниже невозможно:
Вместо этого попробуем найти некоторое β̂, решающее уравнение неидеально, но с минимально возможной ошибкой. Один из способов— минимизировать следующую целевую функцию, являющуюся функцией от β̂.
Минимизация этой суммы квадратов отклонений и дает имя задаче наименьших квадратов. Взятие производных по β̂ и приравнивание к нулю приведут к нормальным уравнениям и предоставят решение в замкнутой форме.
Это один из способов. Но можно использовать линейную алгебру. И вот здесь QR-разложение подойдет как нельзя лучше.
QR-разложение
Для начала давайте опишем это разложение. QR-разложение позволяет отобразить матрицу как произведение двух отдельных матриц Q и R.
Q — ортогональная матрица, а R — треугольная матрица.
Это означает, что:
Так как R квадратная, до тех пор, пока диагональные элементы не равны нулю, она также обратима. Если столбцы X линейно независимы, это всегда будет верным. Хотя, если в данных есть коллинеарность, все же будут возникать проблемы. Тем не менее — и в этом суть QR-разложения — прямоугольная и необратимая X может быть выражена как две обратимые матрицы! И вот это уже имеет смысл.
Решение задачи наименьших квадратов с помощью QR-разложения.
Теперь, зная, что из себя представляет QR-разложение, решим задачу наименьших квадратов следующим образом:
Следовательно:
Это означает, что все, что нужно сделать — это найти матрицу, обратную R, транспонировать Q и вычислить их произведение. Мы получим коэффициенты обычного метода наименьших квадратов. Нам даже не нужно вычислять ковариационную матрицу и обратную ей, что происходит в решении обычным методом наименьших квадратов.
Реализация QR-разложения
Чтобы найти QR-коэффициенты матрицы, сначала найдем Q, используя процесс Грама-Шмидта, затем просто умножим исходную матрицу на транспонированную Q, чтобы найти R. Далее применим QR-разложение, используя функции, внедренные в R и C++. Позднее мы заглянем внутрь этих функций, чтобы рассмотреть весь процесс в деталях.
Я использую две функции: myQRR и myQRCpp, применяющие процесс Грама-Шмидта для QR-разложения. Одна функция написана на R, а другая на C++, она загружается в среду R через Rcpp. В конце статьи я сравню их производительность.
library(Rcpp)
library(tidyverse)
library(microbenchmark)
sourceCpp("../source-code/myQRC.cpp")
source("../source-code/myQRR.R")
Начнем с маленького примера, в котором смоделируем y и X, а затем решим уравнение, используя QR-разложение. Также мы сможем провести двойную проверку QR-разложения — работает ли оно и возвращает ли смоделированный X. Вот смоделированные переменные ответа:
y = rnorm(6)
y
## [1] 0.6914727 2.4810138 0.4049580 0.3117301 0.6084374 1.4778950
Вот данные, которые мы используем для определения коэффициентов наименьших квадратов. В нашем распоряжении 3 переменные:
X = matrix(c(3, 2, 3, 2, -1, 4,
5, 1, -5, 4, 2, 1,
9, -3, 2 , -1, 8, 1), ncol = 3)
X
## [,1] [,2] [,3]
## [1,] 3 5 9
## [2,] 2 1 -3
## [3,] 3 -5 2
## [4,] 2 4 -1
## [5,] -1 2 8
## [6,] 4 1 1
Теперь, чтобы найти Q и R, используем myQRCpp.
Q = myQRCpp(X)$Q
R = t(Q) %*% X %>% round(14)
R
## [,1] [,2] [,3]
## [1,] 6.557439 1.829983 3.202470
## [2,] 0.000000 8.285600 4.723802
## [3,] 0.000000 0.000000 11.288484
Q
## [,1] [,2] [,3]
## [1,] 0.4574957 0.50241272 0.45724344
## [2,] 0.3049971 0.05332872 -0.37459932
## [3,] 0.4574957 -0.70450052 0.34218986
## [4,] 0.3049971 0.41540270 -0.34894183
## [5,] -0.1524986 0.27506395 0.63684585
## [6,] 0.6099943 -0.01403387 -0.07859294
2. Убеждаемся в ортогональности Q.
t(Q)%*%Q %>% round(14)
## [,1] [,2] [,3]
## [1,] 1 0 0
## [2,] 0 1 0
## [3,] 0 0 1
3. И в том, что QR действительно возвращает исходную матрицу X.
Q %*% R
## [,1] [,2] [,3]
## [1,] 3 5 9
## [2,] 2 1 -3
## [3,] 3 -5 2
## [4,] 2 4 -1
## [5,] -1 2 8
## [6,] 4 1 1
Теперь вычисляем актуальные коэффициенты.
beta_qr = solve(R) %*% t(Q) %*% y
beta_qr
## [,1]
## [1,] 0.32297414
## [2,] 0.07255123
## [3,] -0.02764668
Чтобы проверить, верен ли ответ, сравним вычисленное значение β̂ с тем, что выдает функция lm.
coef(lm(y ~ -1 + ., data = data.frame(cbind(y,X))))
## V2 V3 V4
## 0.32297414 0.07255123 -0.02764668
Мы получили в точности то же решение, что и для рассчитанных коэффициентов.
Реализация QR-разложения
Процесс Грама-ШмидтаПроцесс Грама-Шмидта — это метод вычисления ортогональной матрицы Q, которая состоит из ортогональных или независимых единичных векторов и занимает такое же пространство, что и матрица X.
- В качестве начального шага алгоритм включает в себя выбор вектора столбца X, скажем, x1 = u1.
- Затем находим вектор, ортогональный u1, проецируя на него следующий столбец X, скажем, x2, и вычитая из него проекцию u2 = x2 − proj u1x2. Теперь у нас есть набор из двух ортогональных векторов.
- Следующий шаг — проделать то же самое, но вычитая сумму проекций на каждый вектор из набора ортогональных векторов uk.
Выразим это следующим образом:
Получив полный набор ортогональных векторов, просто делим каждый вектор на его нормаль и помещаем их в матрицу:
Зная Q, легко вычисляем R:
Реализация в R и C++
Конечно, в R существуют встроенные функции, осуществляющие QR-разложение. Так как алгоритм Грама-Шмидта является итеративным по своей природе, я решил реализовать его на C++ , являющемся хорошим инструментом для подобных задач, и сравнить его с подобной функцией R. Вот как выглядит моя версия R:
myQR = function(A){
dimU = dim(A)
U = matrix(nrow = dimU[1], ncol = dimU[2])
U[,1] = A[,1]
for(k in 2:dimU[2]){
subt = 0
j = 1
while(j < k){
subt = subt + proj(U[,j], A[,k])
j = j + 1
}
U[,k] = A[,k] - subt
}
Q = apply(U, 2, function(x) x/sqrt(sum(x^2)))
R = round(t(Q) %*% A, 10)
return(list(Q = Q, R = R, U = U))
}
Очень точно. Внутри цикла for есть цикл while, и вызываемая проекционная функция также является функцией, написанной на R.
А вот как выглядит моя версия C++. Логика по сути та же, за исключением того, что есть другой цикл for, нормализующий ортогональные столбцы.
// [[Rcpp::export]]
List myQRCpp(NumericMatrix A) {
int a = A.rows();
int b = A.cols();
NumericMatrix U(a,b);
NumericMatrix Q(a,b);
NumericMatrix R(a,b);
NumericMatrix::Column Ucol1 = U(_ , 0);
NumericMatrix::Column Acol1 = A(_ , 0);
Ucol1 = Acol1;
for(int i = 1; i < b; i++){
NumericMatrix::Column Ucol = U(_ , i);
NumericMatrix::Column Acol = A(_ , i);
NumericVector subt(a);
int j = 0;
while(j < i){
NumericVector uj = U(_ , j);
NumericVector ai = A(_ , i);
subt = subt + projC(uj, ai);
j++;
}
Ucol = Acol - subt;
}
for(int i = 0; i < b; i++){
NumericMatrix::Column ui = U(_ , i);
NumericMatrix::Column qi = Q(_ , i);
double sum2_ui = 0;
for(int j = 0; j < a; j++){
sum2_ui = sum2_ui + ui[j]*ui[j];
}
qi = ui/sqrt(sum2_ui);
}
List L = List::create(Named("Q") = Q , _["U"] = U);
return L;
}
Сравнение реализаций на R и C++
В дополнение к двум функциям выше у меня есть третья, идентичная R, только она называется projC, а не proj. Я назвал ее myQRC (projC написана на C++, а proj — на R). В противном случае у нас есть чистая C++ функция myQRCpp и чистая R функция myQR.
Чтобы сравнить, как быстро эти три функции выполняют QR-разложение, я поместил их в функцию QR_comp, которая вызывает функции и измеряет время выполнения каждой с одним и тем же аргументом матрицы.
QR_comp = function(A){
t0 = Sys.time()
myQR(A)
tQR = Sys.time() - t0
t0 = Sys.time()
myQRC(A)
tQRC = Sys.time() - t0
t0 = Sys.time()
myQRCpp(A)
tQRCpp = Sys.time() - t0
return(data.frame(tQR = as.numeric(tQR),
tQRC = as.numeric(tQRC),
tQRCpp = as.numeric(tQRCpp)))
}
Их производительность можно сравнить по сетке из случайных матриц n на m. Эти матрицы генерируются при вызове функции QR_comp.
grid = expand.grid(n = seq(10, 3010, 500),
m = seq(50, 600, 50))
tvec = map2(grid$n,
grid$m,
~QR_comp(matrix(runif(.x*.y), ncol = .y)))
Наконец, визуализируем.
plotly::ggplotly(
bind_rows(tvec) %>%
gather("func","time") %>%
mutate(n = rep(grid$n, 3),
m = rep(grid$m, 3)) %>%
ggplot(aes(m, n, fill = time)) +
geom_tile() +
facet_grid(.~func) +
scale_fill_gradientn(colours = rainbow(9)) +
theme(panel.background = element_blank(),
axis.ticks.y = element_blank(),
axis.text.y = element_text(angle = 35, size = 5),
axis.text.x = element_text(angle = 30, size = 5)), width = 550, heigh = 400)
Очевидно, что чем больше задействован C++ , тем быстрее вычисление QR-разложения. Функция C++ решает его менее, чем за минуту, для матриц размером до 250 столбцов на 3000 строк или 600 столбцов на 500. R-функция в 2–3 раза медленнее.
Заключение
QR — это просто разложение матрицы, а метод наименьших квадратов просто одно из применений QR. Надеюсь, обсуждение выше демонстрирует, насколько важна и полезна линейная алгебра для науки о данных.
Перевод статьи Ben Denis Shaffer: QR Matrix Factorization
Комментарии