Алгоритм поиска A*

Пошаговый разбор алгоритма поиска А*

Поиск короткого пути — это то, чем каждый занимается ежедневно. Алгоритм А *— один из самых популярных методов решения задач на поиск кратчайшего маршрута. Его относят к информированным алгоритмам поиска, так как для решения задач используются данные о стоимости пути и принципы эвристики.

Алгоритм А* обладает двумя ключевыми характеристиками алгоритмов такого рода: оптимальность и полнота.

Если алгоритм поиска характеризуется как оптимальный, значит он гарантирует получение лучшего из возможных решений. А когда среди характеристик присутствует определение «полный», это означает, что алгоритм всегда находит решение, если таковое существует.

Для понимания работы алгоритма А* необходимо владеть следующими терминами:

— Узел (или вершина) — все потенциальные уникальные позиции или остановки.

— Переход — само перемещение между вершинами или узлами.

— Начальный узел — тот, от которого начинается путь.

— Конечный узел  — тот, в котором путь должен завершиться.

— Пространство поиска — коллекция всех допустимых узлов.

— Стоимость — числовое значение (например, расстояние, время или денежная стоимость), характеризующее отрезок пути от одного узла к другому.

— g(n) — стоимость пути от начальной вершины до любой другой.

— h(n) — эвристическое приближение стоимости пути от узла n до конечного узла.

— f(n) — минимальная стоимость перехода в соседний узел.

Каждый раз при посещении узла подсчитывается его стоимость f(n) (за n принимается соседний узел). Таким образом, алгоритм посещает все соседние узлы и высчитывает тот, у которого данный показатель минимален.

Формула выглядит следующим образом:

f(n) = g(n) + h(n)

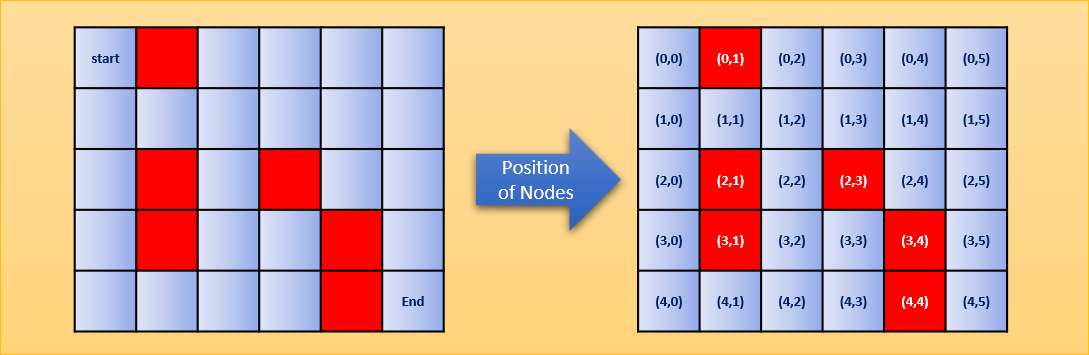
Разберём алгоритм на примере лабиринта с начальным и конечным узлами.

1) Слева: заданный лабиринт 2) Справа: позиция каждого узла (место в массиве) в лабиринте

В лабиринте можно двигаться в четырёх направлениях (влево, вправо, вверх и вниз). Перемещение по красным клеткам запрещено. Таким образом, из стартовой позиции можно сдвинуться только вниз: движение вверх и влево заблокировано стенами, а вправо — красным квадратом.

Сначала создадим класс и вспомогательную функцию:

1. Класс Node используем, чтобы создать объект для каждого узла с информацией о вершине-родителе, актуальном положении в лабиринте и стоимости (g,h,f).

2. Определяем функцию пути, которая будет возвращать значение маршрута от начального до конечного узла.

3. Программируем функцию поиска, отвечающую за логику процесса:

3.1 Инициализируем переменные.

3.2 Добавляем начальную точку в «список посещения». Задаём стоп-условия, чтобы избежать бесконечного цикла. Задаём правила перемещения по позициям.

3.3 Нижеследующее повторяется, пока не сработает стоп-условие:

3.3.1 Выбираем клетку из «списка посещения» с минимальным показателем f. Эта позиция становится текущей. Проверяем, было ли достигнуто максимальное число итераций.

3.3.2 Проверяем, соответствует ли текущая клетка конечному квадрату-цели (то есть был ли определен маршрут).

3.3.3 Проверяем четыре клетки, прилегающих к текущей позиции. Если это тупик или уже посещенные клетки, игнорируем их. В противном случае создаём новый узел, для которого в качестве узла-родителя принимаем текущую клетку и обновляем позицию дочернего узла.

3.3.4 Проверяем все созданные дочерние узлы:

— если его нет в «списке посещения», то добавляем. Текущий узел становится узлом-родителем. Записываем стоимость f, g и h.

— если узел уже есть в списке, проверяем, будет ли путь через него лучше по показателю g (меняем родительский квадрат на текущий и пересчитываем g и f).

4. Основная программа: создаём лабиринт, начальную и конечную позиции. Потом применяем функцию поиска и, если выход существует, он будет отображен.

Теперь рассмотрим пошагово код.

Сначала создаём класс для узла, который будет содержать следующие атрибуты: родительский узел, положение узла и все три стоимости (g, h и f). Потом инициализируем узел и создаем метод для проверки равенства вершин.

Определяем функцию пути, которая будет возвращать значение маршрута от начального до конечного узла.

Теперь определяем функцию поиска. Первый шаг—инициализация узлов и списков, которые будут использоваться.

Добавляем начальный узел в «список посещения». Определяем стоп-условие, чтобы избежать бесконечного цикла. Задаём параметры перемещения относительно текущей позиции, которые будет использоваться для поиска дочернего узла и других возможных перемещений.

Теперь мы используем текущий узел, сравнивая все стоимости f, чтобы выбрать для перехода узел с минимальным показателем. На этом этапе важно проверить, достигнуто ли максимальное число итераций.

Удаляем выбранный узел из «списка посещений» и добавляем в список уже посещенных. Теперь проверяем, был ли найден целевой квадрат. Если ответ положительный, вызываем функцию path.

Для выбранной вершины находим все дочерние элементы. Фиксируем текущую позицию для выбранного узла (теперь узел-родитель):

 а) проверяем, куда возможен переход (не было ли выхода за стену лабиринта);

 б) если переход из позиции заблокирован (например, красный квадрат), тогда игнорируем этот вариант;

 в) добавляем в список допустимых дочерних узлов для выбранного родителя.

На диаграмме чёрная точка — текущий узел, зелёные — дочерние узлы.

Для всех дочерних узлов:

 а) если дочерний элемент уже находится в «списке посещения», игнорируем его и переходим к следующему;

б) вычисляем значения дочерних узлов g, h и f. Стоимость h для текущего узла вычисляется с использованием евклидова расстояния;

в) если дочерний узел уже в «списке посещения», игнорируем его. В противном случае добавляем дочерний узел в список.

Можно запускать программу. Путь будет показан стрелочками.

Заключение

Алгоритм A * — это мощный алгоритм в сфере ИИ с широким спектром применения. Это самый популярный способ для нахождения кратчайшего пути, так как система реализации чрезвычайно гибкая. Сегодня этот алгоритм применяют в различных областях от машинного обучения до разработки игр, например, при выстраивании маршрута по сложной местности с препятствиями.

---

Перевод статьи