Плотность вероятности - это не сама вероятность
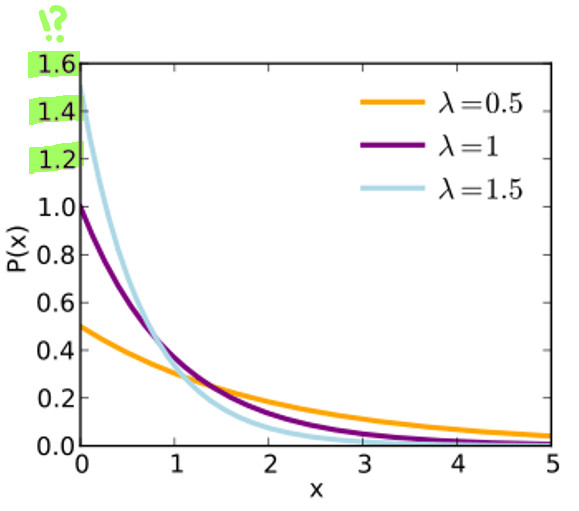
Наибольшее значение вероятности — единица. Это общеизвестный факт! Однако для некоторых плотностей вероятности (например, плотности вероятности экспоненциального распределения на графике ниже), когда λ= 1.5 и ???? = 0 плотность вероятности 1.5, что очевидно больше 1!
1. Почему так?
Даже если плотность вероятности f(x) принимает значение больше 1, если область, в которую она интегрируется, меньше 1, то она сводится к 1. Рассмотрим пример простой плотности вероятности — непрерывное равномерное распределение в области [0, 0.5]. Плотность вероятности непрерывного распределения 1/(b-a) постоянно равна 2.
Непрерывное равномерное распределениеПолная вероятность — это площадь области под графиком f(x),то есть 2*0.5 = 1. Как видите, даже если плотность вероятности больше 1, то при интегрировании в область меньше 1 она сводится к 1.
2. Плотность вероятности и вероятность
Разве плотность вероятности f(x) не есть сама вероятность? Нет. Потому что f(x) может быть больше 1. f(????) — это просто высота графика плотности вероятности при X = ????.
Вся путаница “плотность вероятности = вероятность” возникает из-за того, что мы привыкли к понятию “функция вероятности = вероятность”, что верно. Однако плотность вероятности не то же самое, что функция вероятности. Ее не стоит интерпретировать так же, потому что дискретные и непрерывные случайные величины определяются по-разному.
Чтобы найти вероятность P(????=????) для дискретных случайных величин, мы ищем значение функции вероятности в одной точке. Вот так — в Пуассоновском распределении. Для непрерывных случайных величин мы берем интеграл от плотности вероятности на конкретном промежутке, чтобы найти вероятность того, что X попадет в этот промежуток.
f(x) ≠ P(X = ????)
* f(x): плотность вероятности для непрерывных случайных величин
* P(X = x): функция вероятности для дискретных случайных величин
Теперь, конечно, все понятно. Однако вы можете задаться вопросом… Почему мы должны интегрировать плотность вероятности? Можем ли мы просто суммировать значения плотности, как делаем это со значениями функции вероятности?
Нет. Потому, что для непрерывных случайных величин вероятность того, что ???? принимает какое-либо конкретное значение ???? равна 0. Ниже подробности.
3. Непрерывная случайная величина и вероятность
Посмотрим на предыдущий пример, непрерывное равномерное распределение в [0, 0.5]. Плотность вероятности при x=1 равна двум. Но почему вероятностьпри x=1 нулевая? Чтобы ответить на этот вопрос, нужно сначала ответить на другой. Сколько всего чисел в области [0, 0.5]?
Бесконечность. Бесконечное множество, если быть математически точной. 0.1, 0.01, 0.001, 0.0001, … Можно продолжать вставлять 0 перед единицей. Следовательно, непрерывная случайная величина имеет бесконечное число возможных значений, даже если область определения невелика и фиксирована. Допустим, плотность вероятности для каждого значения на промежутке [0, 0.5] имеет экстремально малое значение, например, 000000001. Тем не менее, сумма бесконечного числа значений достигнет бесконечности независимо от того, насколько малы эти значения. Значит, чтобы получить сумму вероятностей, равную 1, вероятность в каждой конкретной точке должна быть 1/∞, то есть 0.
Это тоже не имеет смысла. Если добавить бесконечное число нулей, все равно получится нуль. Полная вероятность должна составлять единицу, а не нуль.
Дело в том, что нельзя использовать понятие дискретной функции вероятности (у одного значения одна вероятность) для непрерывных величин. Нельзя определить вероятность непрерывных величин таким же образом, что и дискретных.
4. Вероятность из плотности вероятности
Заимствуем идею в интегрированииЕсли вероятность того, что X находится точно в точке ????, равна нулю, как насчет очень маленького интервала вокруг точки ????? Например, [????, ????+d????]? Пусть d???? будет 0.00000000001. Тогда вероятность того, что X попадет в интервал [????, ????+d????] — это область под кривой f(????) расположенной между [????, ????+d????]. Если d???? бесконечно мало, этого приближения достаточно для P(????=????).
f(????)d???? : Вероятность X в [????, ????+d????].
f(????): Плотность вероятности.
d???? : Размер интервала.
Несколько замечаний:
- Если вы посмотрите определения плотности вероятности и функции вероятности, то увидите, что сумма в случае дискретных величин (функция вероятности) меняется на интегралы в случае непрерывных величин (плотность вероятности).
- Почему используются термины «плотность» и «масса»? В физике мы интегрируем плотность для получения массы. Если думать о массе как о вероятности, то мы интегрируем плотность вероятности, чтобы получить вероятность (массу).
- Что означает плотность вероятности в точке ????? Она означает то, насколько вероятность сконцентрирована на единицу длины (d????) вблизи ????, или насколько плотна вероятность вблизи ????.
- Нужно исправить график экспоненциального распределения в англоязычной Википедии. P(X) звучит как вероятность. Нужно изменить эту надпись на f(x) или «Плотность вероятности».
Перевод статьи Aerin Kim: PDF is not a probability
Комментарии