Сумма экспоненциальных случайных величин

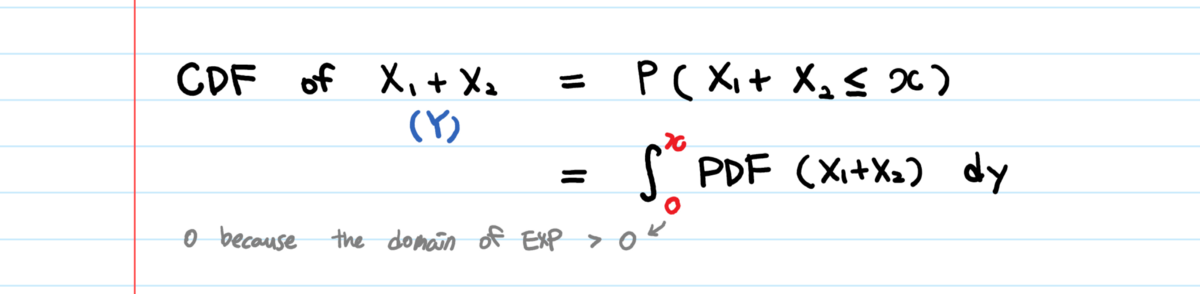
Сумма экспоненциальных случайных величин

Пусть X1 и X2 — независимые, экспоненциальные и случайные величины со средним значением λ. Пусть Y=X1+X2. Тильда (~) означает “имеет распределение вероятностей”, например, X1~EXP(λ). Итак:

X1~EXP(λ)X2~EXP(λ)Y=(X1+X2)

Вопрос: Какова плотность вероятности Y?Где можно использовать распределение Y?

Поиск плотности вероятности.

???? Находим функцию кумулятивного распределения и дифференцируем её. Мы уже использовали этот метод много раз. Затем найдем функцию распределения (X1 + X2):

Но мы не знаем плотности вероятности (X1+X2). На самом деле именно ее мы и хотим вычислить. Хм… может…

∫ PDF(X1+ X2) = ∫ PDF(X1) + ∫ PDF(X2) ???!?!?

Нет, конечно. Если сделать так, плотность вероятности (X1+X2) будет равна 2. Но интеграл плотности вероятности всегда должен быть равен 1. Как теперь найти функцию распределения, не зная плотности вероятности?

Расчет вероятности

Существуют два основных метода. Первый — маргинализация X1 (чтобы мы смогли интегрировать его по ????1). Во втором используется определение независимости: P(????1+????2 ≤ ????|????1) = P(????1+????2 ≤ ????). Эти методы упрощают дифференцирование и помогают получить результат для ????.

В чем отличие ???? от ?????

Это математические соглашения. ???? — стохастическое, а ???? —  детерминированное. Допустим, ???? —число, которое мы получили, бросив кубик. То есть ???? может быть любым числом из множества {1,2,3,4,5,6}. Но как только кубик брошен, значение ???? определено. ???? = ???? означает, что случайная величина ???? принимает конкретное значение ????. Итак:

• ???? — случайная величина, обозначаемая заглавной буквой.
• ???? — определенное (фиксированное) значение, которое может принимать случайная величина. Например, ????1, ????2, …, ????n может быть выборкой, соответствующей случайной величине X.

Следовательно, совокупная вероятность P(???? ≤ ????) означает, что диапазон функции ???? меньше определенного значения ????. При этом ???? может быть любым скаляром, например, ???? ≤ 1, ???? ≤ 2.5, ???? ≤ 888 и т.д.

Плотность вероятности через функцию распределения

Найдём производную функции распределения, чтобы найти плотность вероятности. Это распределение Эрланга:

Применение

В распределении Пуассона со средним значением λ X1+X2 будет отображать время, когда произойдет второе событие. В нашем примере с ???? лайками, если вы получаете лайки со средним значением λ в единицу времени, то время до первого читателя, поставившего лайк, распределяется по экспоненте со средним значением λ. Если вы будете ждать лайков множество единиц времени, то увидите 0, 1, 2, … читателей.

Как долго нужно ждать, чтобы увидеть n читателей, поставивших лайк? Для ответа на этот вопрос используется распределение Эрланга.

Ответом будет сумма независимых экспоненциально распределенных случайных величин, то есть распределение Эрланга (n, λ). Распределение Эрланга  —  частный случай гамма-распределения. Разница между ними в том, что в гамма-распределении n может быть дробным числом.

Упражнения ????

• Какое распределение эквивалентно распределению Эрланга (1, λ)?

Это просто. Экспоненциальное.

• Теория массового обслуживания. Вы идете в закусочную и встаете в очередь, перед вами два человека. Одного обслуживают, другой ждет. Интервалы времени их обслуживания S1 и S2 являются независимыми, экспоненциальными и случайными величинами со средним значением 2 минуты.

Это означает, что среднее значение скорости обслуживания 0,5 в минуту. О связи времени с количеством событий можно подробнее прочитать здесь. Итак, условное время в очереди T = S1 + S2. С учётом состояния системы N = 2. T подчиняется распределению Эрланга.

Какова вероятность того, что вы простоите в очереди более 5 минут? 

Давайте подставим λ = 0.5 в функцию распределения, которую мы уже вывели:

Вероятность того, что вы будете ждать более 5 минут, менее 30%. Классно звучит! 

Заключение

Доктор Богнар из Университета Айовы создал полезный и красивый калькулятор распределения Эрланга (гамма-распределения): 

Цифры совпадают с нашим выводом!

---

Перевод статьи Aerin Kim: Sum of Exponential Random Variables